2.4.4. Homotētija
Īpašība H1. Ja viena taisne l homotētijā attēlojas par taisni l1, tad vai nu l1 sakrīt ar l, vai arī l1||
l.
Īpašība H2. Ja viena riņķa līnija ω homotētijā ar centru O
attēlojas par riņķa līniju ω1
un homotētijas centrs O atrodas uz ω, tad vai nu ω1 sakrīt ar ω (ja homotētijas koeficients ir 1), vai arī ω1
un ω pieskaras viena otrai punktā O.
Īpašība H3. Ja homotētijas koeficients nav 1, tad vienīgais punkts, kas homotētijā paliek uz vietas, ir homotētijas centrs. (Piezīme:
šī īpašība ir acīmredzama.)
Īpašība H4. Ja vispirms izpilda homotētiju (O1; k1)
un pēc tam – homotētiju (O2;
k2), tad:
1) Ja k1· k2
1, tad rezultātā ir izpildīta homotētija ar koeficientu k1· k2.
Tās centru var konstruēt, izmantojot O1;
k1; O2; k2.
2) Ja k1· k2 = 1, tad rezultātā ir izpildīta paralēlā pārnese.
Īpašība H5. Homotētija nemaina figūras orientāciju (skat. īpašības
P3 formulējumu).
Paralēlā pārnese nemaina figūras orientāciju, t.i., ja 3 punkti A, B,
C atrodas pulksteņa rādītāja kustības virzienā, tad arī to attēli A1, B1, C1
atrodas pulksteņa rādītāja kustības virzienā.
Iespējas ar homotētiju attēlot vienu figūru par citu ir plašākas nekā citiem pārveidojumiem, jo homotētija var mainīt ne tikai figūras atrašanās vietu, bet arī tās izmērus.
Homotētija nogriežņu attēlošanā
Ja divi nogriežņi nav paralēli un neatrodas uz vienas taisnes, tad homotētijā tos nevar attēlot vienu par otru.
Pieņemsim, ka divi nogriežņi AB un A1B1
ir paralēli (tātad, neatrodas uz vienas taisnes). Tad gandrīz vienmēr eksistē viena un tikai viena homotētija, kas attēlo AB par A1B1
tā, ka A→A1 un
B→B1. Homotētijas centra O atrašana atkarīga no tā, vai vektori 
un 
ir vienādi vai pretēji vērsti.
Gadījumā a) homotētijas koeficients ir pozitīvs, gadījumā b) – negatīvs.
Homotētija trijstūru attēlošanā
Ļoti liela nozīme ir sekojošai teorēmai, ko mēs minam bez pierādījuma.
Teorēma par homotētiskiem trijstūriem. Ja trijstūra ABC
malas ir attiecīgi paralēlas trijstūra A1B1C1 malām, tad (ar vienu izņēmumu) eksistē homotētija, kurā A → A1,
B → B1
, C → C1
. Vienīgais izņēmums – ja trijstūri ir vienādi un atbilstošās malas arī ir vienādi vērstas (t.i.,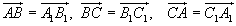
). Tādā gadījumā homotētijas vietā eksistē paralēlā pārnese.
Piezīme. Rezultāts ir spēkā arī, ja trijstūri nav vienādi, un vienā vai divos pāros Atbilstošās malas atrodas nevis uz paralēlām taisnēm, bet uz vienas un tās pašas taisnes.
Homotētija riņķa līniju attēlošanā
Ja divas riņķa līnijas nav vienādas, tad vienmēr eksistē tieši divas homotētijas (viena – ar pozitīvu, otra – ar negatīvu koeficientu), kas attēlo pirmo riņķa līniju par otro. Homotētijas koeficienta modulis vienmēr vienāds ar rādiusu attiecību.
Vienādām riņķa līnijām eksistē tikai homotētija ar negatīvo koeficientu (-1); tās centrs atrodas vidū starp abu riņķa līniju centriem. Savukārt pozitīva koeficienta homotētijas „vietā” ir paralēlā pārnese.
Homotētijas centru atrašanās vietas svarīgākajos gadījumos, ja rādiusi nav vienādi.
1. Riņķa līnijas atrodas viena ārpus otras un nepieskaras.
„Pozitīvās” homotētijas centrs ir kopējo ārējo pieskaru krustpunkts, „negatīvās”- kopējo iekšējo pieskaru krustpunkts.
2. Riņķa līnijas ārēji pieskaras.
„Pozitīvās” homotētijas centrs ir kopējo ārējo pieskaru krustpunkts, „negatīvās”- abu riņķa līniju pieskaršanās punkts.
3. Riņķa līnijas krustojas
„Pozitīvās” homotētijas centrs ir kopējo ārējo pieskaru krustpunkts.
4. Riņķa līnijas iekšēji pieskaras.
„Pozitīvās” homotētijas centrs ir pieskaršanās punkts.