V

A    B    D    E    F    G    K    L    M    N    P    V   

Vektors

Par vektoru sauc orientētu (vērstu) nogriezni. Vektors ir noteikts, ja zināms tā garums un vērsums. Vektoru apzīmē ar diviem lielajiem burtiem, liekot virs tiem bultiņu; pirmais burts vienmēr norāda sākumpunktu, bet otrs – galapunktu, piemēram, 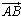, vai arī ar mazo burtu, liekot virs tā bultiņu, piemēram, .

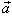Vektora projekcija uz ass

Dots vektors 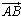. No punktiem A un B velk perpendikulus AA₁ un BB₁ pret asi Ox un AA₂ un BB₂ pret asi Oy. Vektoru 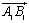sauc par vektora 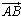ģeometrisko projekciju uz asi Ox, bet vektoru 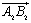par vektora 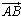ģeometrisko projekciju uz asi Oy. Vektora 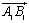(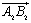) garumu, kas ņemts ar + zīmi, ja 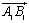(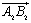) vērsums sakrīt ar Ox (Oy) ass virzienu, vai ar – zīmi, ja 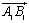(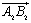) vērsums ir pretējs Ox (Oy) ass vērsumam, sauc par vektora 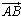algebrisko projekciju jeb vienkārši par vektora 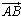projekciju uz Ox (Oy) ass.

Vektora koordinātas

Vektoru plaknē nosaka tā sākumpunkts un beigu punkts. Ja vektora sākumpunkts un galapunkts ir punkti ar koordinātēm A(x₁; y₁) un B(x₂; y₂), tad vektora 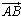koordinātas ir (x₂ -x₁; y₂ -y­₁).

Vērtību apgabals

Kopu, kuras elementi ir visas funkcijas f vērtības f(x), sauc par funkcijas f vērtību apgabalu un apzīmē ar E(f).

Virkne

Par skaitļu virkni (a_n) sauc skaitlisku funkciju f, kuras definīcijas apgabals ir visu naturālo skaitļu kopa N (reizēm definīcijas apgabals var būt kāda naturālo skaitļu kopas apakškopa).

Vienības riņķa līnija

Riņķa līniju, kuras rādiuss ir 1 vienība un centrs atrodas koordinātu sākumpunktā, sauc par vienības riņķa līniju.