1. uzdevums
Dots, ka AB = AB1, AC
= AC1,
BAB1=CAC1=15° , O ir ΔABC
iecentrs
, bet O1 ir
ΔAB1C1 iecentrs. Pierādi, ka OAO1=
15°!
Atrisinājums
No dotā tieši seko, ka punkti B1
un C1 iegūti attiecīgi no B un C, pagriežot tos ap centru A par (-15°).
Tālāk
No tā seko, ka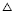 
AB1C1 no 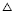ABC šai pašā pagriezienā.
Tālāk
No teorēmas 3
seko, ka tad arī O1
iegūts no O šai pašā pagriezienā; tāpēc OAO1=15°
, k.b.j.
Trijstūrī ievilktās riņķa līnijas centrs.
Ja kādu no mūsu apskatītajiem pārveidojumiem pielieto visiem figūras F punktiem, iegūstot figūru F’, tad katrs figūras F punkts P attēlojas par figūras F’ punktu P’ ar tādu pašu ģeometrisku jēgu, kāda ir punktam P figūrā F (skat.sadaļā 2.3.).